How do we measure distance to stars

Measuring distance in space is not so easy because these distances are so far and it's very difficult to determine how far away one star is from another star. So you are thinking  how do we measure distance to stars & how astronomers measure distances in space and how they measure distance of stars and far and huge galaxies. Yes it is difficult to measure distances in space but not impossible.

we can measure these kind of long distances of stars and galaxies. We've several methods to find several kind of distances.

In other words, astronomers use different methods to determine the distances to objects; the specific method which is used depends on how far away the object is. But all of the methods are wonderful combinations of science and mathematics!

If you are gonna study about how  do they measure distance in space  so first of all we've to learn about measuring unite to measure distances in space. The unit of measuring distance between the stars is known as Astronomical Unite

Astronomical Unit

An Astronomical Unit (AU) is the average distance between Earth and the Sun, which is about 93 million miles or 150 million kilometers. Astronomical units are usually used to measure distances within our Solar System.


how to measure the distance of a star using brightness

 we can determine the real brightness of a star by the color. By knowing the actual brightness and comparing it to the apparent brightness seen from Earth (that is, by looking at how dim the star has become once its light reaches Earth), astronomers can determine the distance to the star.

Radar - Measuring distance in our solar system

This modern method of measuring distances is based on the fact that light (whether in the form of radio waves, microwaves, visible light, or X-rays) travels with a speed of 300,000 km/sec. Therefore, based on the fact that distance traveled equals to the speed at which you travel times the length of time you travel at that speed, we can determine distances in our solar system.

                           d = v x t
where d is distance, v is velocity, and t is time. As mentioned above, when we use any form of light, v is equal to 300,000 km./sec. So if we measure how long it takes for light to go to an object, we can calculate the distance.

This method has been used in one form or another to determine the distances to all of the planets in our solar system (except Pluto, which we have not visited). It is also routinely used to measure the distance from the Earth to the Moon. Mirrors left by Apollo astronauts reflect a laser beam shot from Earth and allow scientists to keep close track on the lunar orbit. The image below shows how the technique works.

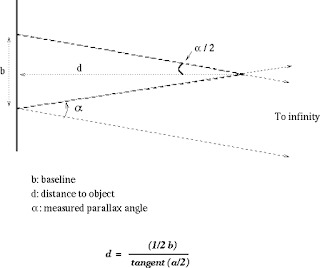
Stellar Parallax - measuring distances to nearby stars

Astronomers derive distances to the nearest stars (closer than about 100 light-years) by a method called stellar parallax. This method that relies on no assumptions other than the geometry of the Earth's orbit around the Sun. You are probably familiar with the phenomenon known as parallax. Try this. Hold out your thumb at arm's length, close one of your eyes, and examine the relative position of your thumb against other distant (background) objects, such as a window, wall, or tree. Now look at your thumb with your other eye. What do you notice? Move your thumb closer to your face and repeat the experiment. What was different this time? This is a demonstration of the parallax effect: the apparent shift in position of a relatively nearby object against more distant ones when viewed from different vantage points.

Now consider that the Earth moves in its orbit around the Sun, allowing us to look at nearby stars from slightly different locations - just like your two eyes are at slightly different locations. This is shown in the image below.
diagram showing how parallax angle is defined based on apparent shift of nearby star as earth orbits the Sun

From the image above, you can see that by knowing the size of Earth's orbit and measuring the angles of the light from the star at two points in the orbit, the distance to the star can be derived. The farther the star is, the smaller the angles. For stars more than about 100 light-years from Earth, we cannot measure any shift and the method fails.

The mathematical formula of a parallax distance is:


Cepheids - measuring distances in our Galaxy and to nearby galaxies

Cepheids, also called Cepheid Variables, are stars which brigthen and dim periodically. This behavior allows them to be used as cosmic yardsticks out to distances of a few tens of millions of light-years.

In 1912, Henrietta Swan Leavitt noted that 25 stars, called Cepheid stars, in the Magellanic cloud would brighten and dim periodically. Leavitt was able to measure the period of each star by measuring the timing of its ups and downs in brightness. What she determined was that the brighter the Cepheid, the longer its period. In fact, Cepheids are very special variable stars because their period (the time they take to brighten, dim and brighten again) is

  • regular (that is, does not change with time), and

  • a uniform function of their brightness. That is, there is relation between the period and brightness such that once the period is known, the brightness can be inferred.


Cepheids are reasonably abundant and very bright. Astronomers can identify them not only in our Galaxy, but in other nearby galaxies as well. If one requires the distance to a given galaxy one first locates the Cepheid variables in this galaxy. From these observations one determines the period of each of these stars. Leavitt's data states that a given period has a unique brightness associated to it. So from the period and Leavitt's plot we get the brightness at the distance of one light-year (see the image above). We can also measure the brightness on Earth. The brightness at the distance of one light-year will be larger than the observed brightness due to the fact that brightness drops like the square of the distance. From these numbers one can extract the distance to the stars. This method works up to 13 million light-years when Earth-bound telescopes are used; for larger distances these stars become too dim to be observed. Recently, space-based telescopes such as the Hubble Telescope, have used these stars to much farther distances. Looking at a galaxy in the Virgo cluster called M100, astronomers used the Cepheid variables observed there to determine its distance - 56 million light-years.
 to other galaxies

Supernovae - measuring distances to other galaxies

At large distances (up to about 1 billion light-years), astronomers can no longer use methods such as parallax or Cepheid variables. At such large distances, the parallax shift becomes too small and we can no longer even see individual stars in galaxies. Astronomers then turn to a series of methods that use "standard candles", that is, objects whose absolute magnitude is thought to be very well known. Then, by comparing the relative intensity of light observed from the object with that expected based on its assumed absolute magnitude, the inverse square law for light intensity can be used to infer the distance. The unique characteristics and enormous brightness of a certain type of supernova, the explosion which can occur at the end of the main sequence life of a massive star, can be used to determine distances beyond the reach of the previous methods.

There have been many measurements of the manner in which a supernova, whose distance to Earth is known (using one of the previous methods), increases its brightness and then dims into oblivion. There is one type (called type Ia) for which this brightening and dimming is very regular: when the maximum brightness at a distance of 1 light-year is calculated (using the known distance and the 1/distance2 rule), it is found to be about the same for all stars. Such Type Ia supernovae are then our standard candles.

If the distance to a far away galaxy is required, one must first locate a type Ia supernova in it (which do occur regularly) and then measure its observed brightness. Comparing this result with the known maximum brightness achieved by all such supernovae one can determine the distance to the galaxy in question (again using the 1/distance2 rule). Since supernovae are extremely bright, this method is useful to very large distances, up to one billion light-years.

Redshift and Hubble's Law - measuring distances to objects far, far away

For very far objects (beyond about 1 billion light-years) none of the above methods work. Scientists must move from direct observation to using observations in conjunction with a theory. The theory used to determine these very great distances in the universe is based on the discovery by Edwin Hubble that the universe is expanding.

In 1929, Edwin Hubble announced that almost all galaxies appeared to be moving away from us. In fact, he found that the universe was expanding - with all of the galaxies moving away from each other. This phenomenon was observed as a redshift of a galaxy's spectrum. This redshift appeared to be larger for faint, presumably further, galaxies. Hence, the farther a galaxy, the faster it is receding from Earth. You can see this trend in Hubble's data shown in the images above. The velocity of a galaxy could be expressed mathematically as

                    v = H x d

where v is the galaxy's radial outward velocity, d is the galaxy's distance from Earth, and H is the constant of proportionality called the Hubble constant.

The exact value of the Hubble constant is still somewhat uncertain, but is generally believed to be around 65 kilometers per second for every megaparsec in distance. (A megaparsec is given by 1 Mpc = 3 x 106 light-years). This means that a galaxy 1 megaparsec away will be moving away from us at a speed of 65 km/sec, while another galaxy 100 megaparsecs away will be receding at 100 times this speed. So essentially, the Hubble constant reflects the rate at which the universe is expanding.

So to determine an object's distance, we only need to know its velocity. Velocity is measurable thanks to the Doppler shift. By taking the spectrum of a distant object, such as a galaxy, astronomers can see a shift in the lines of its spectrum and from this shift determine its velocity. Putting this velocity into the Hubble equation, they determine the distance. Note that this method of determining distances is based on observation (the shift in the spectrum) and on a theory (Hubble's Law). If the theory is not correct, the distances determined in this way are all nonsense. Most astronomers believe that Hubble's Law does, however, hold true for a large range of distances in the universe.

It should be noted that, on very large scales, Einstein's theory predicts departures from a strictly linear Hubble law. The amount of departure, and the type, depends on the value of the total mass of the universe. In this way a plot of recession velocity (or redshift) vs. distance, which is a straight line at small distances, can tell us about the total amount of matter in the universe and may provide crucial information about the mysterious dark matter.